Übergangsbogen und Überhöhung

Diese Seite beutzt im Abschnitt, der die Berechnung von Übergangsbögen erläutert, zur Darstellung der Formeln MathML. Der Netscape Navigator zeigt diese Formeln ab Version 7.0 an, Firefox tut das natürlich auch (ab Version 1.5). Gegebenfalls wird man aufgefordert, die erforderlichen Fonts herunterzuladen, und zwar hier. Für den Internet Explorer ist ein Plug-in erforderlich, z.B. MathPlayer 2.2 (funktioniert ab IE6.0), der kostenlos hier erhältlich ist, samt den erforderlichen Fonts. Spätestens seit IE Nr. 8 scheint der MathPlayer auch bei Microsoft implementiert. Opera packte es leider lange Zeit gar nicht, die neueren Versionen hängten sich zwar nicht mehr auf, stellten aber die Seite nicht richtig dar - nun, Opera 10 kann es jetzt auch. Nur Google Chrome scheitert, die Formeln werden nicht richtig wiedergegeben.

zurück     Vorbildfotos     Modellfotos     Berechnung     nach unten     nach Hause

"In der Kurve lauert der Tod", so warnte man einst - so ernst geht's bei der Bahn im allgemeinen nicht zu, aber damit der Tod nicht lauert, gilt in der Kurve bekanntlich die Geschwindigkeitsbeschränkung.

Eine Liste der höchstens zulässigen Geschwindigkeiten für verschieden gängige Radien können Sie der Tabelle entnehmen. Maßgebend für die Festlegung dieser Höchst­geschwindigkeiten, die im übrigen seit Jahrzehnten unverändert gelten, ist ausschließlich die Bequemlichkeit der Passagiere. Denen mag man nämlich nur eine ziemlich geringe Querbeschleunigung oder Fliehkraft zumuten, es soll ja im D-Zug nicht zugehen wie im Jahrmarktskarussell. Den Physikunterricht wollen wir hier nicht wiederholen; das Maß für die Beschleunigung ist m/sec², und die maximale zulässige Querbeschleunigung ist 0,85 m/sec² - seit der EBO von 1967, vorher 0,65 m/sec² gemäß der BO von 1928. Das Rad-Schiene-System verträgt weitaus mehr, Entgleisungsgefahr besteht erst ab viel höheren Querbeschleunigungen, aus Unfallanalysen hat man errechnet, dass Entgleisungen erst ab etwa 2 m/sec² drohen; 3 m/sec² würden den Zug aus den Schienen kippen, wenn er noch nicht entgleist ist. Diese Reserve nutzen die modernen Fahrzeuge mit fliehkraftabhängigen Wagenkasten-Neigevorrichtungen.

Aber Geschwindigkeit ist alles, und wie man weiß, kommt man schneller um die Kurve, wenn man sich so richtig in sie hineinlegt. Jeder Radfahrer macht das automatisch, weil durch die Schräglage die Fliehkraft kompensiert wird. Auf diese Idee ist die Bahn auch ziemlich bald gekommen: die Gleisüberhöhung war geboren. Die äußere Schiene wird einfach ein Stück höher gelegt als die innere, und schon legt sich der Zug schön in die Kurve. Im Prinzip gibt's da keine Grenze, ältere Rennsportfans sprechen noch heute feuchten Auges von der berühmt-berüchtigten Steilwandkurve der AVUS. Dass die Eisenbahn sich trotzdem nicht in die Kurve legen darf wie die Achterbahn auf dem Rummel, liegt wieder an der maximal zulässigen Querbeschleunigung - siehe oben -, nur diesmal in der anderen Richtung. Jeder kennt das etwas unangenehme Gefühl, nach innen zu rutschen, wenn der Zug in einer überhöhten Kurve zum Stehen kommt, besonders früher auf den Kunststoff bezügen der 2. Wagenklasse.

Also darf die schon erwähnte größte Querbeschleunigung auch hier wieder nicht höher sein also oben angegeben, nur dass sie jetzt nicht von der Fliehkraft, sondern von der Neigung des in der überhöhten Kurve stehenden Zuges erzeugt wird. Aus diesem Grunde war die maximale Überhöhung bei den deutschen Normalspurbahnen auf 150 mm festgelegt, um so viel darf die bogenäußere Schiene höher liegen als die innere. Erst in jüngster Zeit hat es hier eine Änderung gegeben: Die Überhöhung darf sogar 170 mm betragen, wenn sichergestellt ist, dass Züge regulär dort nicht zum Stehen kommen können, etwa vor einem geschlossenen Signal.

Ideal ist es natürlich, wenn die Fliehkraft in jedem Bogen genau durch die Überhöhung kompensiert ist. In diesem Fall spricht man von ausgeglichener Überhöhung. Diesen Zustand, in dem man die Kurve gar nicht merkt, kann man aber nur herstellen, wenn alle Züge immer mit derselben Geschwindigkeit durchfahren, also z.B. reinen S-Bahn- oder Güterstrecken. Auch die Neubaustrecken der DB sind überwiegend mit ausgeglichener Überhöhung hergestellt. Auf Strecken mit gemischtem Verkehr ist die Sache komplizierter. Die langsameren Güterzüge nutzen im überhöhten Bogen die innere Schiene stärker ab als die äußere, deswegen muss die Überhöhung abhängig von der Belastung durch Güterzüge reduziert werden. Weichen im Bogen führen ebenfalls zu einer Beschränkung (auf 100 mm), Reduzierungen sind ebenfalls er forderlich an Bahnsteiggleisen (maximal 60 mm) und in sehr engen Radien. Auf solchen Strecken wird die höchstens zulässige Geschwindigkeit wieder so festgelegt, dass gerade die maximal zulässige Querbeschleunigung auftritt.

Überhöhungen von weniger als 20 mm werden nicht hergestellt, ergibt die Berechnung einen Wert unter 20 mm, wird die Überhöhung weggelassen. Ferner werden die errechneten Überhöhungen auf die nächsten vollen 5 mm aufgerundet.

Da die Überhöhung ja nicht bei Bogenbeginn plötzlich erklettert werden kann, wird die Überhöhung durch eine Überhöhungsrampe vermittelt. Deren Neigung durfte früher maximal 1 : 300 betragen, heute fordert man 1 : 400, mindestens, angestrebt wird aber als Divisor das Zehnfache der Geschwindigkeit in km/h, also z.B. 1 : 1000 bei 100 km/h. Bei den Neubaustrecken beträgt die Rampenneigung aus Komfortgründen sogar nur 1 : 2000, außerdem sind dort die Übergänge ausgerundet, so dass man eine geschwungene Überhöhungsrampe erhält.

Vor Einführung der Übergangsbögen wurde die Rampe in die Gerade vor den Bogen gelegt, so dass die Überhöhung bei Bogenbeginn hergestellt war, und bei einfachen Anlagen, z.B. Schmalspur- oder einfachen Nebenbahnen, ist dies auch heute noch so.

Wenn man es richtig machen will, wird es ein wenig komplizierter: Theoretisch sollte der Schwerpunkt des Fahrzeuges immer in gleicher Höhe bleiben. Dies herzustellen wäre aber zu aufwendig, was die Vermessung und den Gleisbau betrifft. Deshalb verlegt man auch das überhöhte Bogengleis auf dem ebenen Planum, und zwar meist so, dass die bogeninnere Schiene ihre Höhe behält und nur die äußere sich hebt. Teilweise machte man es sich noch einfacher und nahm die bogeninnere Schwellenende als Bezugspunkt, so dass auch das innere Gleis etwas an gehoben wird; dies Verfahren lässt sich auch im Modell besonders einfach nachahmen.

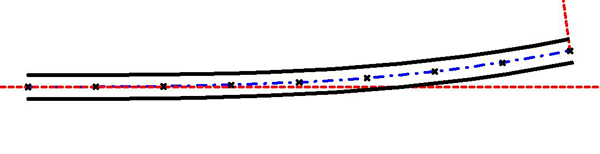
Bei mehrgleisigen Strecken werden die Gleise normalerweise unabhängig voneinander überhöht. Sind Gleise jedoch durch Weichen miteinander verbunden, muss das äußere Gleis so angehoben oder das innere so abgesenkt werden, dass die Schienenköpfe auf einer (schiefen) Ebene liegen. Im Hintergrund der Abb. 5 ist dies zu sehen. Das Gleiche gilt für Bahnübergänge, siehe Abb. 9, jedenfalls in der Regel.

Tabelle 1 zeigt, welche Auswirkung die Überhöhung auf die zulässige Geschwindigkeit der Züge im Bogen hat. Auch ist die Geschwindigkeit angegeben, bei der bei maximaler Überhöhung von 150 mm die Querbeschleunigung genau ausgeglichen ist. Allerdings ist diese Aufstellung ein wenig irreführend, da die rechnerisch möglichen Geschwindigkeiten immer auf den nächsten vollen Fünfer abgerundet werden. So reicht bei einem Radius von 300 m für die maximal möglichen 80 km/h schon eine Überhöhung von 125 mm aus, die vollen 150 mm sind dafür nicht erforderlich. Tabelle 2 zeigt für einige Radien die jeweils mindestens erforderlichen Überhöhungen.

Überhöhung im Modell

In H0 beträgt die maximale Überhöhung 1,7 mm. Das klingt wenig, ist aber eine ganze Menge, wenn man es zur Spurweite von 16,5 mm in Beziehung setzt! Unsere Zeichnungen und Fotos zeigen das. Deshalb ist Sparsamkeit geboten, wenn man Modellgleise überhöht. Eigentlich gilt ja, in Anlehnung an das Vorbild: Je enger der Bogen, desto größer die Überhöhung. Aber probieren Sie es aus: Schieben Sie Holzstückchen unter die Außenkanten eines Industriegleises, Märklin-Grundradius oder ROCO R1! Lange Fahrzeuge wirken in solch engen Bögen schon merkwürdig, aber der Anblick steigert sich ins Groteske, wenn solch ein Bogen auch noch überhöht ist.

Außerdem gibt's da im Modell noch ein Problem: Je mehr die Wagen geneigt sind, desto größer wird die Gefahr, dass sie von der Zugkraft, die an der Kupplung zieht, umgeworfen werden. Es ist nun mal so, dass wenn die Längenmaße 1/87stel des Vorbildes betragen, die Volumina und damit die Massen in der dritten Potenz kleiner werden, also 658503 mal geringer sind! Auch aus diesem Grund setzt die volle Überhöhung auch einen maßstäblichen Radius voraus, und der kleinste Radius, der mit der vollen Überhöhung von 150 mm ausgestattet werden darf, beläuft sich auch beim Vorbild auf immerhin 275 m, darunter muss auch beim Vorbild die Überhöhung vermindert werden, aus ziemlich den gleichen Gründen übrigens.

Sparen Sie sich die Überhöhung also für einen besonderen Effekt auf, eine weite Kurve, eine Krümmung der "Paradestrecke" (so nannte die MIBA. in den sechziger Jahren die lange Gerade im Vordergrund).

Bereits eine kleine Überhöhung von einem Drittel bis zur Hälfte des maximal Möglichen, also 0,5 bis 0,8 mm, hat eine bemerkenswerte Wirkung, man hat schon dann den Eindruck, dass der Zug sich in die Kurve legt wie beim großen Vorbild.

Wie man die überhöhte Kurve im Modell baulich herstellt, darauf gehen wir gleich ein. Zunächst befassen wir und mit der zweiten Hälfte des Themas, dem

Übergangsbogen

Zu Beginn des Eisenbahnbaus wurden Kurven ohne Übergangsbögen ausgeführt, dass heißt, an die Gerade schloss sich unmittelbar der Bogen an. Dies erzeugt einen Ruck, der, als die Geschwindigkeiten größer wurden, zu häufigen Entgleisungen und großen Abnutzungen im Bogeneinlauf führte, so dass schon 1854 Übergangsbögen empfohlen wurden und u.a. bei der Brennerbahn erstmals angewandt wurden. Das heißt, dass man den Radius von der Gerade her schrittweise oder stetig vermindert, bis der endgültige Kurvenradius erreicht ist.

Obwohl Überhöhung und Übergangsbogen zunächst unabhängig voneinander aufkamen, verknüpfte man sehr schnell beides miteinander. Kurz, man verband und verbindet noch heute den Übergangsbogen derart mit der Überhöhungsrampe, dass an jeder Stelle der Radius gerade so groß ist, dass die Fliehkraft der Überhöhung entspricht. Theoretisch ergibt das eine Kurve, die "Bernoullische Lemniskate" heißt, und die war auch der großen Eisenbahn in der Ära der Logarithmentafeln und Rechenschieber zu kompliziert, so dass man statt dessen eine kubische Parabel benutzte. Diese Kurve wiederum ist im Zeitalter der Taschenrechner und PCs so handlich, dass man sie sogar für die Modellbahn benutzen kann, was wir auch gleich tun werden. (Eine weitere Kurve, die man näherungsweise benutzt hat, ist die so genannte Klotoide.) Die Formel der kubischen Parabel lautet:

(1)   y = x³ / 6C

C ist eine Konstante, deren Größe von der Art der Bahn, der gefahrenen Geschwindigkeit und dem kleinsten vorkommenden Radius bestimmt wurde. Einige ausgewählte Größen bringt die nebenstehende Tabelle: Weiteres über Formel und Berechnung nebenan im Kasten, wichtig ist nur noch, dass sich aus der Ableitung der obigen Formel ergibt:

(2)   L = C / R

Liegt die Konstante C einmal fest, kann man zu jedem Radius sehr schnell die Länge des Übergangsbogens ermitteln, also z.B. für preußische Hauptbahnen, C = 12000, ergibt sich bei 300 m Kurvenradius ein Übergangsbogen von 40 m Länge, bei 600 m Radius von nur noch 20 m Länge. Je weiter der Bogen, desto kürzer also der Übergangsbogen, und desto geringer auch die Überhöhung, bis beide bei sehr weiten Kurven ganz wegfallen. Ein weiteres Beispiel: Württemberg. C = 15.000 ergibt bei 300 m Radius eine Rampenlänge von 50 m; bei der dort geltenden maximalen Überhöhung von 125 mm erhielt man eine Rampensteigung von 1 : 400.

Da man heute die Länge der Überhöhungsrampe von der Geschwindigkeit abhängig macht (s.o.), die Neigungswechsel der Überhöhungsrampen ausrundet und überdies andere Rechenverfahren benutzt, lässt sich für heutige Verhältnisse kein einheitlicher Wert für "C" angeben. Er würde für normale Hauptbahnen bei 20.000 - 75.000 liegen.

Übergangsbögen im Modell

Ein C von 12.000 ergäbe bei maßstäblicher Umrechnung ein Modell-C von 1.585.000 in H0 (wenn man in Millimetern rechnet). Mit solchen maßstäblichen Umrechnungen zu arbeiten ist nur sinnvoll, wenn man dies auch sonst im Modell tut. In allen anderen Fällen kommt man zu einem vernünftigen Wert, wenn man die Gleichung (2) umdreht:

(3)   C = L * R

Nehmen wir an, Sie wollen einen Bogen mit 1000 mm Radius überhöhen, und nehmen wir weiter an, Sie wollen die volle Überhöhung nutzen, 1,7 Modellmillimeter (was nicht zu empfehlen wäre). Für die Überhöhungsrampe gilt beim Vorbild eine maximale Steigung von 1 : 300, dieser Wert, der schon beim Vorbild extrem steil ist und heute nicht mehr verwendet wird, ist auch fürs Modell die unterste Grenze; wenn Sie maßstäbliche Schnellzugwagen mit RP25-Radsätzen fahren lassen, wäre 1 : 400 auch im Modell betriebssicherer. Aber bleiben wir für dieses Beispiel bei 1 : 300, dann wir die Überhöhungsrampe 1,7 x 300 = 510 mm lang. Dieses Beispiel ist als drittes im Rechenkasten durchgerechnet und ist auch die Grundlage unserer Zeichnung. Nach der schlichten Formel (2) rechnen wir also mit einer Konstante C von 510.000.

Praktische Durchführung

Für die Herstellung von überhöhten Gleisen im Modell eignet sich ausschließlich Meterware, wenn sie das Gleis nicht gänzlich selbst bauen wollen (siehe MIBA 11/98). Kurvenstücke sind dazu nicht geeignet, weil sie in sich nicht flexibel genug sind, Sie würden das Gleisstück als ganzes um die inneren Ecken kippen. Wie oben bereits erwähnt gab es Bahnen, die die Erhöhung so herstellten, dass sie das innere Ende der Schwelle auf einer Höhe ließen und die ganze Schwelle anhoben; dies Verfahren hat den Nachteil, dass sich auch die bogeninnere Schiene hebt, aber den Vorteil, dass man auch im Bogen eine ebene Trasse benutzen kann. Eben diesen Vorteil kann man auch im Modell nutzen, aber nur bei privaten Nebenbahnen und einfachsten Verhältnissen, das Verfahren war nicht staatsbahnmäßig. Wenn man sich dafür entscheidet, können einige der unten angegebenen Schritte entfallen.

Zunächst einmal stellt man das Planum wie gewohnt her: Trassenbrett und Korkbettung. Auf die Korkbettung zieht man auf der ganzen Länge des Bogens ein schließlich des Übergangsbogens innen und außen eine Linie, 8,5 mm von der Gleismitte. Dann nimmt man Schleifklotz und Schmirgelpapier und schruppt das Korkbett auf der Bogeninnenseite bis zu der inneren Linie schräg herunter.

An die äußere Linie klebt man ein Holzleistchen in der gewünschten Stärke auf, wiederum auf der ganzen Länge des Bogens, aber zunächst noch nicht für den Übergangsbogen. Unter den Northeastern-Profilen findet man eine geeignete Auswahl für diese Zwecke, z.B. 1,6 oder 1,2 oder 0,8 mm.

Im Übergangsbogen muss auch die Höhe dieser Holzleiste kontinuierlich von 0 auf die Endhöhe steigen und am anderen Ende wieder auf 0 sinken. Dies Ergebnis kann man auf verschiedene Weise erzielen, man schneidet, sägt oder feilt die Leiste erst auf Maß und klebt sie dann auf, oder man klebt sie auf und schleift dann. Ich habe sie erst aufgeklebt, aber in Stufen, da ich die Profile zur Hand hatte. Man hat dann einige Fixpunkte, nämlich die Enden der Leisten, an denen man das gleichmäßige Ab- oder Zunehmen der Höhe kontrollieren kann.

Nun kann man nochmals kontrollieren, indem man mit einer Musterschwelle den Bogen entlang fährt, ob man innen überall genug abgeschliffen hat. Dann klebt man auf den so vorbereiteten Unterbau das Gleis.

Berechnung von Übergangsbögen

Dieser Abschnitt befindet sich hinter den Fotos, aus historischen Gründen, die Darstellung der Formeln war noch vor gar nicht all zu langer Zeit ein Problem!

zurück     nach oben     Modellfotos     Berechnung     nach unten     nach Hause

Übersicht Vorbildfotos

UB01 Bei Rhina	UB02 Bei Rhina	UB03 Bei Rhina	UB04 Hedschasbahn	UB05 Hedschasbahn
UB06 218 127-1	UB07 Überhöhte Weiche	UB08 Übergangsbogenweiche	UB09 Bahnübergang	UB10 RhB
UB11 Am Bahnsteig	UB12 WLE	UB13 FSE	UB14 Auf Brücken	UB15
UB16 Oberroden	UB17 Grafing-Stadt

zurück     nach oben     Vorbildfotos     Berechnung     nach unten     nach Hause

Übersicht Modellfotos

MUB01 Holzstreifen	MUB02 Holzstreifen	MUB03 Holzstreifen	MUB04 Holzstreifen	MUB05 Schwellen
MUB06 180 m mit 50 km/h	MUB07 180 m mit 50 km/h	MUB08 180 m mit 50 km/h

zurück     nach oben     Vorbildfotos     Modellfotos     nach unten     nach Hause

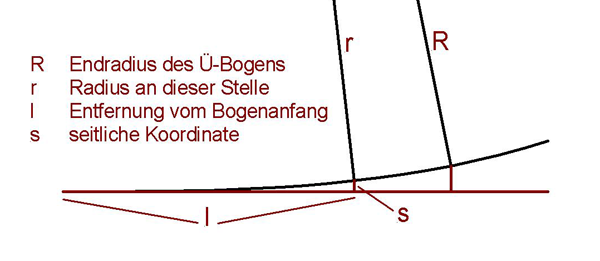
Berechnung von Über­gangs­bögen Dieser Abschnitt benutzt zur Dar­stel­lung der Formeln MathML. Erläuterungen hierzu, ins­beson­dere zur Brauser­kompati­bili­tät gibt es oben auf der Seite. Die Formel der kubischen Parabel lautet: (1)    $y=\frac{x^3}{6C}$ Das heißt, der Abstand s von der Geraden ist in der Ent­fernung l vom Start­punkt: (2)    $s=\frac{l^3}{6C}$ Den Winkel α, genauer: den Tan­gens dieses Winkels an dieser Stelle erhalten wir aus der 1. Ableitung dieser Formel: (3)    $\mathrm{tan \alpha }=\frac{l^2}{2C}$ oder aufgelöst nach α: (3a)    $\alpha =\frac{180}{\pi }\mathrm{atan}\left(\frac{l^2}{2C}\right)$ Die Krümmung, das ist der Kehrwert des Radius, ergibt sich aus der 2. Ableitung der Funk­tion: (4)    $\frac{1}{R}=\frac{l}{C}$ Woraus sich der Radius R für jede Entfernung l vom Anfang des Über­gangs­bogens ergibt: (4a)    $R=\frac{C}{l}$ l gibt die Entfernung vom Start­punkt des Über­gangs­bogens an. Der Bogen selbst ist etwas länger und kann überschlägig berechnet wer­den wie folgt:
	Rechenbeispiele Beispiel 1 (maßstäblich): 300 m Vorbildradius 80 km/h, volle Überhöhung Rampe 1 : 400, C = 1.450.000 Beispiel 2 (maßstäblich): 180 m Vorbildradius 50 km/h, 50 mm Überhöhung Rampe 1 : 400, C = 475.000 Beispiel 3 (unmaßstäblich): 1000 m radius volle Überhöhung Rampe 1 : 300, C = 510.000 Beispiel 4 (unmaßstäblich): 1000 m Modellradius 1 mm Überhöhung Rampe 1 : 400, C = 400.000 l s α ü l s α ü l s α ü l s α ü 50 0,01 0,03 50 0,0 0,15 50 0,04 0,14 50 0,05 100 0,07 0,12 0,25 100 0,35 0,35 0,25 100 0,33 0,56 100 0,42 0,25 150 0,24 0,27 150 0,32 0,56 150 1,10 1,26 0,50 150 1,41 200 0,56 0,48 0,50 200 2,81 2,41 0,50 200 2,61 2,25 0,50 200 3,33 250 1,10 0,75 230 4,25 3,18 0,58 250 5,11 3,51 250 6,51 300 1,89 1,09 0,75 Modell-Endradius (H0): 2069 mm 300 8,82 5,04 1,00 300 11,25 0,75 350 3,01 1,48 350 14,01 6,84 350 17,86 400 4,49 1,93 1,00 400 20,92 8,91 400 26,67 7,59 1,00 450 6,39 2,44 450 29,78 11,23 1,50 Modell-Endradius (H0): 1000 mm 500 8,77 3,01 1,25 500 40,85 13,77 550 11,68 3,64 510 43,35 14,31 1,72 600 15,16 4,33 1,50 Modell-Endradius (H0): 1000 mm 650 19,27 5,08 689 22,93 5,70 1,72 Modell-Endradius (H0): 3448 mm
	Eine Zeichnung zum Beispiel 4 können Sie hier herunterladen

zurück     nach oben     Vorbildfotos     Modellfotos     Berechnung     nach Hause